The Mysterious and Unpredictable RND

Part 3 of several

The Mysterious And Unpredictable RND

Bob Albrecht and George Firedrake

Editor's Note: You may reach Bob & George by mail at:
P. O. Box 310
Menlo Park, CA
94025

Dice Roller

OK PET, let's roll one die a bunch of times. We will simulate rolling an ordinary six-sided die. For each roll, the possible outcomes are 1 or 2 or 3 or 4 or 5 or 6.

100 REM***DICE ROLLER #1
200 REM***FIND OUT HOW MANY ROLLS
210 PRINT "[CLR]" ;
220 INPUT "HOW MANY DICE ROLLS" ; N
400 REM***ROLL ONE DIE N TIMES
410 FOR K = 1 TO N
420 DIE = INT(6*RN(1)) + 1
430 PRINT DIE,
440 NEXT K
450 PRINT
999 END

For many dice games or other uses of dice, we roll two dice. The outcome of a roll is the total of the "spots" or number showing on both dice.

Your turn. Tell PET how to simulate rolling two dice.

Exercise 11. Write a program to simulate rolling two dice, N times.

HOW MANY DICE ROLLS? 20
8	7	3	10
9	9	8	4
6	7	10	11
5	6	5	6
READY
▪

When we roll two dice, the possible outcomes are numbers from 2 to 12. However, they are not equally likely.

There is only one way to get 2.
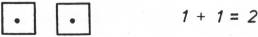
There are two ways to get 3.
There are several ways to get 7.

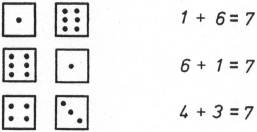
And several more!

Exercise 12. Complete the following table showing the number of different ways to get each possible outcome (2 through 12) in rolling two 6-sided dice.

OUTCOME	NUMBER OF WAYS
2	1
3	2
4	5
5	—
6	—
7	—
8	—
9	—
10	—
11	—
12	—

Next, we would like to compute proportions, as defined below (X is any outcome, 2 through 12).

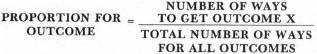
Or, since the total for all outcomes is 36,

Exercise 13. Complete the following table (use a calculator!)

OUTCOME	NUMBER OF WAYS	PROPORTION
2	1	1/36 = .0278
3	2	2/36 = .0556
4	3	3/36 = .0833
5	—	______________
6	—	______________
7	—	______________
8	—	______________
9	—	______________
10	—	______________
11	—	______________
12	—	______________

If we flip a coin, the probability of getting HEADS is ½ = .5. What is the probability of getting TAILS?

Yes, we are leading up to a heavy exercise. But, you can probably do it!

Exercise 14. Write a program to simulate N rolls of two dice. Don't print the results. Instead, count the number of occurrences of each possible outcome (2 through 12), then print this information and also print the proportion of each outcome. Huh? For N rolls, the proportion for outcome X is:

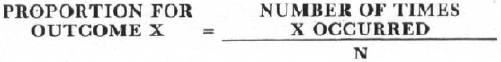
We did it, we wrote the program and ran it. Here is what happened.

OUTCOME FREQUENCY PROPORTION
 2       23        .024
 3       62        .062
 4       81        .081
 5       109       .109
 6       140       .14
 7       142       .142
 8       137       .137
 9       126       .126
 10      80        .08
 11      72        .072
 12      27        .027

If you have the time, try 10000 rolls, or 20000 rolls, or even 100000 rolls. Compare the proportions with the proportions you wrote down for Exercise 13. Or, compare with our answers for Exercise 13.