THE SBC GAZETTE 
AIM 65 BASIC Floating-Point Arithmetic From Machine Language
Paul Beasley,
Mobile, AL
Writing floating-point operations in machine language on a microprocessor is a "messy" proposition. I avoid it like the plague unless I absolutely must do it. But I have discovered how to use the floating-point routines in the AIM 65 BASIC ROM's. It's so easy even I do not mind floating-point applications any more.
AIM 65 BASIC Floating-Point Numbers
For those who are unfamiliar with floating-point numbers, particularly on the AIM 65, I'll describe the floating-point number format. Floating-point representations are similar to scientific notation. An example of a number written in normalized, scientific notation is .27 × 102 ( = 27). Computers commonly use a similar scheme except instead of 10 as a base, the base 2 is used (e.g., 27 = .84375 × 25). By storing the sign, the exponent of 2, and the mantissa of the number, a broad range of values can be efficiently represented. In the AIM 65, this is accomplished by storing each floating-point number in five consecutive bytes as follows:

The exponent, E, is a power of 2 and is biased so that E = $80 actually corresponds to a power of 0, E = $7F corresponds to -1, E = $81 corresponds to + 1, etc. When a floating-point number is normalized, the mantissa is shifted so that the first 1 bit of the mantissa falls in bit position 7 of M3. This means that bit 7 of M3 will always be 1 and the exponent reflects the number of bits that the mantissa was shifted in order to have the implied decimal in front of the first 1 bit. E = $80 means no shifts were required; E = $81 means the mantissa was shifted right one bit; E = $7F means the mantissa was shifted left one bit; etc.
Since bit 7 of M3 is always 1 using the above method, it is stripped off and restored only when performing arithmetic operations (this process is explained later). So, when a number is stored in memory, this bit position is used to store the sign of the number — 0 for positive and 1 for negative. (Incidentally, the floating-point representation of 0 is all five bytes equal $00.) My previous example of the number 27 would be stored in memory as follows:
85 58 00 00 00
AIM 65 BASIC Floating-Point Accumulators
In order to use floating-point numbers in arithmetic operations, BASIC reserves twelve bytes in Page 0 to provide two floating-point accumulators. Accumulator 1 (FPAC1) is in locations $A9 through $AE and accumulator 2 (FPAC2) is in locations $B 1 through $B6. Each accumulator spans six bytes and has the following format:

As I mentioned earlier, when numbers are stored into memory, the sign is put into bit 7 of M3. Technically, this is accomplished as follows:
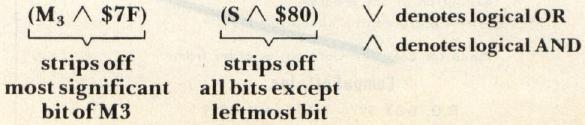
| Table 1. Calling sequences for floating-point operations. | |||
| OPERATION | CALLING SEQUENCE | ||
| 1. Load FPAC1 | LDA | AL | |
| LDY | AH | source address | |
| JSR | $C8E1 | ||
| 2. Load FPAC2 | LDA | AL | |
| LDY | AH | source address | |
| JSR | $C7CB | ||
| 3. Store FPAC1 | LDX | AL | |
| LDY | AH | destination address | |
| JSR | $C913 | ||
| 4. Copy FPAC1 to FPAC2 | JSR | $C94B | |
| 5. Copy FPAC2 to FPAC1 | JSR | $C93B | |
| 6. Convert fixed-point to floating-point | LDY | IL | |
| LDA | IH (result in FPAC1) |
||
| 7. Convert floating-point to fixed-point | Load FPAC1 with floating-point value | ||
| JSR | $C536 | ||
| (result right-justified in M3-M0 of FPAC1 | |||
| 8. Addition | Load FPAC1 with operand 1 | ||
| LDA | AL | source address for minuend | |
| LDY | AH | ||
| JSR | $C58F | ||
| (Addressed value is loaded into FPAC2, FPAC1 is subtracted from FPAC2 and result in FPAC1; FPAC2 unchanged.) | |||
| 10. Multiplication | Load FPAC1 with operand 1 | ||
| Load FPAC2 with operand 2 | |||
| JSR $C76F | |||
| (result in FPAC1; FPAC2 unchanged.) | |||
| 11. Division | Load FPAC1 with divisor | ||
| Load FPAC2 with dividend | |||
| JSR | $C851 | ||
| (result in FPAC1; FPAC2 unchanged.) | |||
| 12. Power operation | Load FPAC1 with exponent | ||
| Load FPAC2 with base number | |||
| JSR | $CC7F | ||
| (FPAC2 is riased to the power in FPAC1; result in FPAC1; FPAC2 unchanged.) | |||
| 13. Multiply FPAC1 by 10; | JSR | $C821 | |
| 14. Divide FPAC1 by 10 | JSR | $C83D | |
| 15. Add .5 to FPAC1 | JSR | $C588 | |
| 16. Convert floating-point number to ASCII string | Load FPAC1 with number | ||
| JSR | $CB1C | ||
| (result at $0200) | |||
| Note: Resulting ASCII string starts at location $0200. The first character is a space, followed by the ASCII digits and ended with a $00 byte. | |||
| 17. Compare FPAC1 to memory | LDA | AL | source address of number in memory |
| LDY | AH | ||
| Branch to xxxx if: | JSR | $C99A | |
| memory < FPAC1 | BCC | xxxx | |
| memory = FPAC1 | BEQ | xxxx | |
| BEQ | LABEL | ||
| memory >FPAC1 | BCS | xxxx | |
| LABEL | . | ||
| . | |||
| . |
| Table 2. Intrinsic Function Subroutine Addresses | ||
| Basic Function | Address | Description |
| ABS | $C997 | Absolute Value of FPAC1 |
| COS | $CDD2 | Cosine of FPAC1 |
| EXP | $CCF1 | Raises e to power in FPAC1 |
| INT | $CA0B | Integer portion of FPAC1 |
| LOG | $C729 | Natural logarithm of FPAC1 |
| NEG | $CCB8 | Negation of FPAC1 |
| RND | $CD96 | Generates random number |
| SGN | $C978 | Sign function of FPAC1 |
| SIN | $CDD9 | Sine of FPAC1 |
| SQR | $CC75 | Square root of FPAC1 |
| TAN | $CE22 | Tangent of FPAC1 |
The logical OR places the sign bit into M3.
When a number is loaded into one of the accumulators, the sign bit is separated out and made the sixth byte of the accumulator (as shown above) so that bit 7 of M3 can be restored to 1. This makes arithmetic operations easier and explains why the accumulators are six bytes each. My example of the number 27 would appear in an accumulator as:
85 D8 00 00 00 00
In addition to the accumulators, there are two other bytes in Page 0 that you should know about. These are the overflow (at $B0) and underflow (at $B8) bytes. The underflow byte is used for rounding M0 of FPAC 1. The overflow byte becomes non-zero when a computational result becomes too large. It is important that these two bytes be initialized to zero before the first floating-point operation is performed. In relation to this, I must give a word of caution. The BASIC floating-point routines still "think" they are operating in the context of a BASIC program. This means that any computation error (e.g., overflow) which is normally trapped by BASIC will still be caught and your program terminated. The termination message may look peculiar since the BASIC statement and variable pointers in Page 0 probably contain meaningless values.
Performing The Floating-Point Operations
I have prepared Table 1 as a reference for the fundamental floating-point operations along with their appropriate machine language calling sequences. All operations are executed with the subroutine jump instruction (JSR) plus minimal parameter set-up. In preparing the table I used the following notation:
AL–Address Low; the least significant 8 bits of the source or destination memory address.
AH–Address High; the most significant 8 bits of the source or destination memory address.
IL–Integer Low; the memory address of the least significant 8 bits of a 2-byte integer value.
IH–Integer High; the memory address of the most significant 8 bits of a 2-byte integer value.
FPAC1–Floating Point Accumulator 1.
FPAC2–Floating Point Accumulator 2.
In addition to the fundamental operations in Table 1, the BASIC intrinsic functions may also be used. The common calling sequence for these functions is as follows:
load FPAC1 with the argument value JSR $xxxx (select function address from Table 2) (result in FPAC1)
The entry point address for each of the functions is given in Table 2.
Sample Program
In order to illustrate what I have just described, I have included the following sample program. It is a very simple calculation of the volume of a cylinder using the formula V = π r2h, where r = radius and h = height. I know that r2 can be computed as r times r very efficiently, but I used the power function to illustrate its use. When the program finishes (successfully), it will display V = 88357.2935. Another tidbit I'll point out is that the floating-point representation for 2 π is at location $CE53 of the BASIC ROM's.
Sample Program: Calculate Volume of Cylinder (V = π r2h)
* = $0220
COMIN = $R1A1 ; monitor entry for command input
EQUAL = $E7D8 ; output "=" to display/printer
OUTPUT = $E97A ; output char.in A to diaplay/printer
CRLOW = $EA13 ; output CR & LF to display/printer
FMUL = $C76F ; floating-point multiply
CONVIF = $C0D1 ; convert fixed-point to floating-point
CONVFA = $CB1C ; convert floating-point to ASCII string
FST1 = $C913 ; store FPAC1
FLD2 = $C7CB ; load FPAC2
CPY12 = $C94B ; copy FPAC1 to FPAC2
FDIV = $C851 ; division
FPWR = $CC7F ; power operation
PI2 = $CE53 ; 2*
START LDY R ; get radius
LDA #0
STA $B8 ; initialize underflow
STA $B0 ; and overflow bytes
JSR CONVIF
LDX #<TEMP
LDY #>TEMP
JSR FST1 ; store R in TEMP
LDY #2
LDA #0
JSR CONVIF ; exponent 2 in FPAC 1
LDA #<TEMP
LDY #>TEMP
JSR FLD2 ; load R in FPAC2
JSR FPWR ; raise R to power 2
LDX #<TEMP
LDY #>TEMP
JSR FST1 ; store R squared in TEMP
LDY H
LDA #0
JSR CONVIF ; height H in FPAC 1
LDA #<TEMP
LDY #>TEMP
JSR FLD2 ; load FPAC2 with R squared
JSR FMUL ; FPAC1 = H times R squared
LDA #<PI2
LDY #>PI2
JSR FLD2 ; load 2* innto FPAC2
JSR FMUL ; FPAC1 = H times R squared times 2
JSR CPY12 ; save FPAC1 in FPAC2
LDY #2
LDA #0
JSR CONVIF ; FPAC1=2
JSR FDIV ; divide by 2
JSR CONVFA ; resulting volume in FPAC1
JSR CRLOW
LDA #'V'
JSR OUTPUT ; display 'V'
JSR EQUAL ; display '='
LDX #0
LABEL 1 LDA $0200,X ; fetch & display ASCII digits
BEQ LABEL2
JSR OUTPUT
INX
JMP LABEL1
LABEL 2 JSR CRLOW
JMP COMIN
R .BYTE 25 ; radius = 25
H .BYTE 45 ; height = 45
TEMP .BYTE 0,0,0,0,0
.END