Rubik's Cube Solved
Dieter Kuespert
Glendale, AZ
Do you have a mixed-up Rubik's Cube sitting around? Your computer can tell you how to solve it step-by-step. There are versions of the solution here for PET/CBM and Atari — it requires 16K RAM memory. The author will make a tape copy (for Commodore machines only) for $3 if you don't want to type it in.
Here is a general solution for the problem of the Rubik's Cube. It absolutely does not matter what the combination of colors is on your cube when the program is started. There are differently designed cubes on the market having a variety of color combinations on the various planes.
The only deviation from the generality is the requirement that you use the letter "W" for white. If this is not done, the program assumes a wrong input. There is this required initial condition under all circumstances:
White has to be in the middle of the upper plane! Throughout the whole procedure it is mandatory that only single slices are turned, never the cube as a whole.
The program has been written in BASIC only. It is for use with a PET/CBM computer. As, however, no unusual program techniques are used, it should not cause any difficulties to adapt it to other Microsoft computers. Due to its generality, it was not possible to fit the program into 8K of memory. It takes about 14K instead, which permits use of a 16K computer.
At the start the program requests the color combination of the cube as it exists. A question mark appears in the respective field for which the first letter of the relevant color has to be keyed in. This has to be done carefully, as no correction is possible except to restart the program from the beginning. In practice it has proven unnecessary to provide a correction routine. The cube is displayed as if it were folded open. The letter "W" is also displayed as a reminder. It is easy to assign the fields to the cube accordingly.
After input of the last letter, the program starts to check for the fields of the white plane, which will appear on top of the cube after the appropriate instructions have been executed.
The cube will subsequently be solved in slices from top to bottom. The number of necessary moves is not optimized because this would require more than 16K of memory. Therefore, in order to find a field of a certain color, you are asked to turn slices until this color appears at a certain spot which is the only one checked every time. This will require some additional moves.
The subroutines necessary for keeping track of all fields are grouped at the end of the program. There is one for each kind of turn. The display of the required turn is connected to the exchange routine. After the display is on the CRT, the exchange is performed by the program. At the same time the plane of the actual cube is turned by the player. Thus the time is used in an optimal way. After the cube is solved, the computer so indicates.
As this is a rather long program, I am willing to save you the boring work of typing all those GOSUBs. Just send a tape or disk and $3 for a copy. (PET/CBM machines only.) Don't forget to include a self-addressed, stamped mailer.
Dieter Kuespert
4333 W. Sandra Circle
Glendale, AZ 85308
|
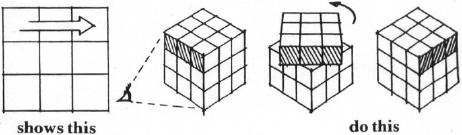
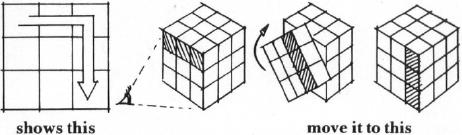
How To Follow The Computer's Instructions: You must keep the same face of the cube towards you at all times. Start with white in the middle of the upper (facing the ceiling) face. As you make the moves, imagine that the cube is held firmly in a vice in the same position throughout. Rotate individual slices, but the whole cube stays in position from start to finish. An "arrow" will appear on screen for each move, and you respond by turning the slice on which the arrow sits in the direction the arrow points. Turn one rotation only per move. (See Figure 1.) If the computer wants you to turn that slice three times, the arrow will reappear in the same place three times. There are only two other possible moves: the front (the side closest to your body) and rear faces (the one furthest away from you). If a strange "curved" arrow appears, that means that you should rotate the entire front face one move in the direction the arrow curves. To perform the same move for the back side, the computer will announce that you should turn the rear side. The arrow will appear curved as it does for a front-side rotation. (See Figure 2.) It sounds a little complicated, but it isn't when you get started. There are really only two different types of moves to make. The computer will wait until you have moved; then you hit a key, and it announces the next move. |
Atari Notes
Because of the extreme length of this program, a full converted program is not feasible. Instead, use the following suggestions to convert Rubik's Cube Solver to the Atari as you are typing it in. If von prefer, you can type in the program first, LIST it to tape or disk, and then use an Editor (such as the Atari Assembler/Editor Cartridge) with search and replace to make "global" changes to the text. You can then use ENTER to read the converted program with BASIC.
- Change all occurrences of "NEXT" without a variable to "NEXT I".
- Text preceded with "[RVS]" should be entered using the Atari Logo key.
- PRINT statements with die [HOME] character should be rephrased:
from: PRINT"[HOME][06 RIGHT]" to: POSITION 0,0:PRINT"[06 RIGHT]"
- All TAB statements should be converted as in:
from: PRINT TAB(TB);T$ to: POKE85,TB:PRINT T$
- The PRINT statements to draw the arrows will have to he converted for use with Atari keyboard graphics. (See below.)
- (JET statements such as:
GET B$(K):IF B$(K) = "" THEN
should be changed to:
GET#1,A:B$(K+ 1, K+1) = CHR$(A) (see below)
- Substitute line 150 below, and add line 100:
100 GRAPHICS 0 : POKE 752,1 : POKE 82,0: OPEN#1, 4, 0,"K:" 150 DIM A$(10), B$(10), C$(10), D$(10), E$(10), F$(10), T$(10), U$(l0)
- Strings (of course) will have to be changed. Generally, all references to variable xx$(n) will become xx$(n + 1, n + 1). For example,
1170 IF C$(4) = D$(5) THEN 1190
becomes
1170 IF C$(5,5) = D$(6,6) THEN 1190
Here's where SEAR.C11 and REPLACE come in handy. Just use ten patterns, such as:
REP/$(0)/$(1, 1)/, A
Watch out for statements like A$(I), which should become A$(I +1, I + 1), or A$(10-K), which should be A$(11-K,11-K).