A BCD to Floating-Point Binary Routine
Marvin L. De Jong
Department of Mathematics-Physics
The School of the Ozarks
Pt. Lookout, MO 65726
Introduction
The principal purpose of this article is to provide the reader with a program that converts a BCD number (ASCII representation) with a decimal point and/or an exponent to a floating-point binary number. The floating-point binary number has a mantissa of 32 bits, an exponent byte consisting of a sign bit and seven magnitude bits, and a sign flag (one byte) for the mantissa. Positive and negative numbers whose magnitudes vary from 1.70141183*1038 to 1.46936795*10-39 and zero can be handled by this routine. In subsequent articles I hope to provide an output routine and a four-function arithmetic routine. The routine described here could be used in conjunction with the Am9511 Arithmetic Processing Unit1 to perform a large variety of arithmetic functions.
Floating-Point Notation
Integer arithmetic is relatively simple to do with the 6502. Consult the Bibliography for a number of sources of information on multiple-byte, signed number addition, subtraction, multiplication and division. Scanlon's book, in particular, has some valuable assembly language routines of this sort. However, additional problems arise when the decimal number has a fractional part, such as the "14159" in the number 3.14159. Also, integer arithmetic is not suitable for handling large numbers like 2.3*1015. The solution is to convert decimal numbers to floating-point binary numbers. A binary floating-point number consists of a mantissa with an implied binary point just to the left of the most-significant non-zero bit and an exponent (or characteristic) that contains the information about where the binary point must be moved to represent the number correctly. Readers who are familiar with scientific notation will understand this quickly. Scanlon's book has a good section on floating-point notation. We will merely illustrate what a decimal number becomes in floating point binary by referring you to Table 1. The dashed line over a sequence of digits means that they repeat. For examples, 1/3 = .
| Table 1. Decimal number to floating-point binary conversions. | ||||
| NUMBER | BINARY NUMBER | FLOATING POINT NOTATION | MANTISSA | EXPONENT |
| 0 | 0 | 0 × 20 | 0 | 0 |
| 1 | 1 | .1 × 21 | 1 | 1 |
| 2 | 10 | .1 × 22 | 1 | 10 |
| 4 | 100 | .1 × 23 | 1 | 11 |
| 1.5 | 1.1 | .11 × 21 | 11 | 1 |
| 0.75 | .11 | .11 × 20 | 11 | 0 |
| 0.1 | 0.0001100 |
. |
-11 | |
| 31 | 11111 | .11111 × 25 | 11111 | 101 |
| 32 | 100000 | 100000 | 1 | 110 |
A close examination of Table 1 yields some important conclusions. Unless a number is an integer power of two (2n where n is an integer), the mantissa required to correctly represent the number will require more bits as the numbers increase. Thus, the number 1 can be correctly represented with a one-bit mantissa, but the number 31 requires a five-bit mantissa. A n-bit mantissa can correctly represent a number as large as 2n - 1, but no larger. There is another problem associated with numbers like 0.1ten that become repeating numbers in binary. It should be clear that no mantissa with a finite number of bits can represent 0.1 exactly. The fact that computers use a finite number of bits to represent numbers like 0.1 can be illustrated by using BASIC to add 0.1 to a sum and print the answer repeatedly. Starting with a sum of zero, we obtained an answer of 3.6 after 36 times through the loop, but the next answer is 3.69999999 which is clearly incorrect. The error incurred by using a finite number of bits, to represent a number that requires more than that number of bits to correctly represent it, is called roundoff error.
How many bits should be used for the mantissa? Clearly it should be an integer number of bytes for ease in programming. Some computers have software packages that use a 24 bit mantissa. The largest number that can be represented by 24 bits is 224 -1 = 16777215. This represents about seven decimal digits, giving about six digit accuracy after several calculations. With my salary there is no trouble with six digit accuracy, but many financial calculations require accuracy to the nearest cent, and six digits are frequently not enough. If we choose 32 bits for our mantissa size we get a little more than nine digits (4.3 × 109). This is the mantissa size used in several versions of Microsoft BASIC, and it is the size chosen here. The propagation of round-off errors through the calculations normally gives about eight digit accuracy. It is generally true that the roundoff errors accumulate as the number of calculations to find a specific result increases, but this is a subject beyond the scope of this article.
How big should the exponent be? If we choose to represent the binary exponent with one byte then we will have seven bits to represent the exponent (one sign bit and seven magnitude bits). The largest exponent is then +127. If all the bits in the mantissa are ones, then the largest number that can be represented is (1/2 + 1/4 + 1/8 + 1/16 + .... + 1/232)*2127, which is approximately 1.70141183*1038. The smallest exponent is -128. The smallest positive number that the mantissa can be is 1/2, thus the smallest positive number that can be represented is 2-129 which is approximately 1.46936795*10-39. Of course, if we chose to use two bytes for the exponent then much larger and smaller exponents could be accommodated, but for most calculations by earth people, a range of 10-39 to 1038 will do quite nicely. Remember that if you try to enter a number whose absolute value is outside of the range just given (except for zero) you will obtain erroneous results. No overflow or underflow messages are given when entering numbers with this routine.
One more note before turning to the program. The mantissa is said to be normalized when it is shifted so that the most-significant bit is one, and the binary point is assumed to be to the left of the most-significant bit. The only exception to this is the number zero which is represented by zeros in both the mantissa and the exponent. Although you are free to assume the binary point is some other place in the mantissa, it is conventional to keep it to the left of the mantissa, as illustrated in Table 1.
The Program To Float A Number
The program in Listing 1, written in the form of a subroutine, together with the other subroutines given in the listings, will accept numbers represented by ASCII from an input device and convert the numbers into their floating point representation. A typical entry might be + 12.3456789E + 24 or -.123456789E-30. The plus sign is optional since the computer simply disregards it. Up to 12 significant digits may be entered, although the least-significant three will soon be disregarded, leaving approximately 9 decimal digits (32 binary digits). At the completion of the routine, the floating-point representation will be found in locations $0001, $0002, $0003, $0004 (mantissa), $0005 (exponent) and location $0007 contains the sign of the mantissa. The sign byte is $FF if the number is negative, otherwise it is $00. Note that the accumulator (locations $0001-$0004) has not been complemented in the case of a minus number. Forming the twos complement may be done, when required, by the arithmetic routines. If a format compatible with the Am9511 Arithmetic Processing Unit is required, simply drop the least-significant byte of the mantissa ($0004), put the sign (set the bit for a minus, clear it for a plus) in bit seven of the exponent ($0005) and shift the sign of the exponent from bit seven to bit six, making sure to keep the rest of the exponent intact. Table 2 gives a summary of the important memory locations.
| Table 2. Memory assignments for the BCD to floating-point binary routine. |
| $0000 = OVFLO; overflow byte for the accumulator when it is shifted left or multiplied by ten. |
| $0001 = MSB; most-significant byte of the accumulator. |
| $0002 = NMSB; next-most-significant byte of the accumulator. |
| $0003 = NLSB; next-least-significant byte of the accumulator. |
| $0004 = LSB; least-significant byte of the accumulator. |
| $0005 = BEXP; contains the binary exponent, bit seven is the sign bit. |
| $0006 = CHAR; used to store the character input from the keyboard. |
| $0007 = MFLAG; set to $FF when a minus sign is entered. |
| $0008 = DPFLAG; decimal point flag, set when decimal point is entered. |
| $000A = ESIGN; set to $FF when a minus sign is entered for the exponent. |
| $000B = TEMP; temporary storage location. |
| $000C = EVAL; value of the decimal exponent entered after the "E." |
| $0017 = DEXP; current value of the decimal exponent. |
After clearing all of the memory locations that will be used by routine, the program in Listing 1 jumps to a subroutine at $0F9B. Most users will not want to call this subroutine, since it merely serves to clear the AIM 65 display. Subroutine INPUT, called next, must be supplied by the user. It must get a BCD digit represented in ASCII code from some input device, store it in CHAR at $0006, and return to the calling program with the ASCII character in the 6502's accumulator. The necessary subroutines for the AIM 65 are given in Listing 4. They are given in the "K" disassembly format with no comments since they have previously been described by De Jong2. Our subroutines input the number on the keyboard and echo the number on the printer and the display.
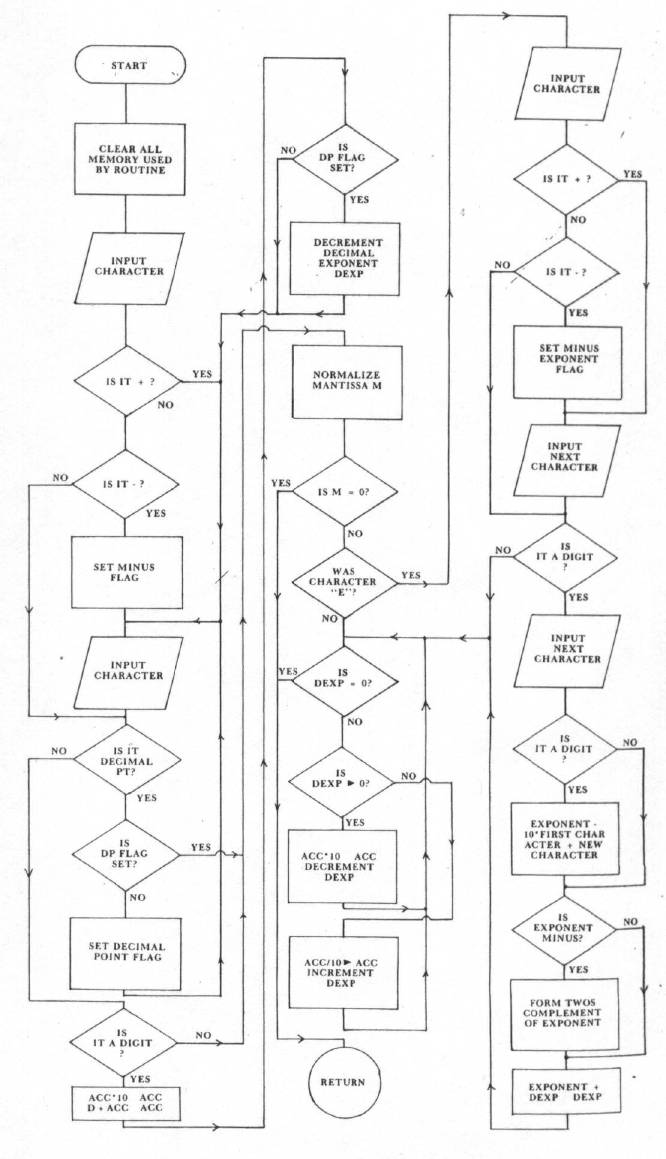
The algorithm for the conversion routine was obtained from an article by Hashizume3. If you are interested in more details regarding floating-point arithmetic routines, please consult his fine article. A flow chart of the routine in Listing 1 is given in Figure 1. The flow chart and the program comments should be sufficient explanation. Basically it works by converting the number, as it is being entered, to binary and multiplying by ten, in binary of course. Later, if and when the exponent is entered, the number is either multiplied or divided by ten, in binary, to get a normalized mantissa and an exponent representing a power of two rather than a power often. Each time a multiplication or division by ten occurs the mantissa is renormalized and rounded upward if the most-significant discarded bit is one. Each normalization adjusts the binary exponent. When the decimal exponent finally reaches zero no more multiplications or divisions are necessary since 100 = 1. To maintain 32-bit precision, an extra byte, called OVFLO, is used in the accumulator for all *10 and /10 operations.
REFERENCES
1. De Jong, Marvin L., "Interfacing the Am9511 Arithmetic Processing Unit," COMPUTE II. (in press).
2. De Jong, Marvin L., "An AIM 65 Notepad," MICRO, No. 16, Sept. 1979, p. 11.
3. Hashizume, Burt, "Floating Point Arithmetic," BYTE, V 2, No. 11, Nov. 1977, p. 76.
BIBLIOGRAPHY
1. Programming and Interfacing the 6502, With Experiments, Marvin L. De Jong, Howard W. Sams & Co., Indianapolis, 1980.
2. 6502 Assembly Language Programming, Lance A. Leventhal, Osborne/McGraw-Hill, Berkeley, 1979.
3. 6502 Software Design, Leo J. Scanlon, Howard W. Sams & Co., Indianapolis, 1980.
| Listing 1. ASCII to Floating-Point Binary Conversion Program | |||
| $0E00 D8 | START | CLD | Decimal mode not required |
| 0E01 A2 20 | LDX $20 | Clear all the memory locations used for storage by this routine by loading them with zeros. | |
| 0E03 A9 00 | LDA $00 | ||
| 0E05 95 00 | CLEAR | STA MEM,X | |
| 0E07 CA | DEX | ||
| 0E08 10 FB | BPL CLEAR | ||
| 0E0A 20 9B 0F | JSR CLDISP | Clears AIM 65 display. | |
| 0E0D 20 30 0F | JSR INPUT | Get ASCII representation of BCD digit. Is it a + sign? Yes, get another character. Is it a minus sign? | |
| 0E10 C9 2B | CMP $2B | ||
| 0E12 F0 06 | BEQ PLUS | ||
| 0E14 C9 2D | CMP $2D | ||
| 0E16 D0 05 | BNE NTMNS | ||
| 0E18 C6 07 | DEC MFLAG | Yes, set minus flag to $FF. | |
| 0E1A 20 30 0F | PLUS | JSR INPUT | Get the next character. |
| 0E1D C9 2E | NTMNS | CMP $2E | Is character a decimal point? |
| 0E1F D0 08 | BNE DIGIT | No. Perhaps it is a digit. Yes, check flag. | |
| 0E21 A5 08 | LDA DPFLAG | Was the decimal point flag set? | |
| 0E23 D0 2C | BNE NORMIZ | Time to normalize the mantissa. | |
| 0E25 E6 08 | INC DPFLAG | Set decimal point flag, and get the next character. | |
| 0E27 D0 F1 | BNE PLUS | ||
| 0E29 C9 30 | DIGIT | CMP $30 | Is the character a digit? |
| 0E2B 90 24 | BCC NORMIZ | No, then normalize the mantissa. | |
| 0E2D C9 3A | CMP $3A | Digits have ASCII representations between $30 and $39. | |
| 0E2F B0 20 | BCS NORMIZ | ||
| 0E31 20 00 0D | JSR TENX | It was a digit, so multiply the accumulator by ten and add the new digit. First strip the ASCII prefix by subtracting $30. | |
| 0E34 A5 06 | LDA CHAR | ||
| 0E36 38 | SEC | ||
| 0E37 E9 30 | SBC $30 | ||
| 0E39 18 | CLC | Add the new digit to the least- significant byte of the accumulator. | |
| 0E3A 65 04 | ADC LSB | ||
| 0E3C 85 04 | STA LSB | Next, any "carry" will be added to the other bytes of the accumulator. | |
| 0E3E A2 03 | LDX $03 | ||
| $0E40 A9 00 | ADDIG | LDA $00 | |
| 0E42 75 00 | ADC ACC,X | Add carry here. | |
| 0E44 95 00 | STA ACC,X | And save result. | |
| 0E46 CA | DEX | ||
| 0E47 10 F7 | BPL ADDIG | The new digit has been added. | |
| 0E49 A5 08 | LDA DPFLAG | Check the decimal point flag. | |
| 0E4B F0 CD | BEQ PLUS | If not set, get another character. | |
| 0E4D C6 17 | DEC DEXP | If set, decrement the exponent, then get another character. | |
| 0E4F 30 C9 | BMI PLUS | ||
| 0E51 20 30 0D NORMIZJSR NORM | Normalize the mantissa. | ||
| 0E54 84 0B | STY TEMP | Save Y. It contained the number of "left shifts" in NORM. | |
| 0E56 A9 20 | LDA $20 | ||
| 0E58 38 | SEC | The binary exponent is 32 - number of left shifts that NORM took to make the most-significant bit one. | |
| 0E59 E5 0B | SBC TEMP | ||
| 0E5B 85 05 | STA BEXP | ||
| 0E5D A5 01 | LDA MSB | If the MSB of the accumulator is zero, then the number is zero, and its all over. Otherwise, check if the last character was an "E". | |
| 0E5F F0 5A | BEQ FINISH | ||
| 0E61 A5 06 | LDA CHAR | ||
| 0E63 C9 45 | CMP $45 | ||
| 0E65 D0 52 | BNE TENPRW | If not, move to TENPRW. | |
| 0E67 20 30 0F | JSR INPUT | If so, get another character. | |
| 0E6A C9 2B | CMP $2B | Is it a plus? | |
| 0E6C F0 06 | BEQ PAST | Yes, then get another character. | |
| 0E6E C9 2D | CMP $2D | Perhaps it was a minus? | |
| 0E70 D0 05 | BNE NUMP | No, then maybe it was a number. | |
| 0E72 C6 0A | DEC ESIGN | Set exponent sign flag. | |
| 0E74 20 30 0F | PAST | JSR INPUT | Get another character. |
| 0E77 C9 30 | NUMB | CMP $30 | Is it a digit? |
| 0E79 90 3E | BCC TENPRW | No, more to TENPRW. | |
| 0E7B C9 3A | CMP $3A | ||
| 0E7D B0 3A | BCS TENPRW | ||
| 0E7F 38 | SEC | It was a digit, so strip ASCII prefix. | |
| $0E80 E9 30 | SBC $30 | ASCII prefix is $30. | |
| 0E82 85 0B | STA TEMP | Keep the first digit here. | |
| 0E84 20 30 0F | JSR INPUT | Get another character. | |
| 0E87 C9 30 | CMP $30 | Is it a digit? | |
| 0E89 90 13 | BCC HERE | No. Then finish handling the exponent. | |
| 0E8B C9 3A | CMP $3A | ||
| 0E8D B0 0F | BCS HERE | ||
| 0E8F 38 | SEC | Yes. Decimal exponent is new digit plus 10 times the old digit. | |
| 0E90 E9 30 | SBC $30 | ||
| 0E92 85 0C | STA EVAL | Strip ASCII prefix from new digit. | |
| 0E94 A5 0B | LDA TEMP | Get the old character and multiply it by ten. First times two. | |
| 0E96 0A | ASL A | ||
| 0E97 0A | ASL A | Times two again makes times four. | |
| 0E98 18 | CLC | ||
| 0E99 65 0B | ADC TEMP | Added to itself makes times five. | |
| 0E9B 0A | ASL A | Times two again makes time ten. | |
| 0E9C 85 0B | STA TEMP | Store it. | |
| 0E9E 18 | HERE | CLC | Add the new digit, to the exponent. |
| 0E9F A5 0B | LDA TEMP | ||
| 0EA1 65 0C | ADC EVAL | ||
| 0EA3 85 0C | STA EVAL | Here is the exponent, except for its sign. Was it a negative? | |
| 0EA5 A5 0A | LDA ESIGN | ||
| 0EA7 F0 09 | BEQ POSTV | No. | |
| 0EA9 A5 0C | LDA EVAL | Yes, then form its twos complement by complementation followed by adding one. | |
| 0EAB 49 FF | EOR $FF | ||
| 0EAD 38 | SEC | ||
| 0EAE 69 00 | ADC $00 | ||
| 0EB0 85 0C | STA EVAL | Result into exponent value location. | |
| 0EB2 18 | POSTV | CLC | Prepare to add exponents. |
| 0EB3 A5 0C | LDA EVAL | Get "E" exponent. | |
| 0EB5 65 17 | ADC DEXP | Add exponent from input and norm. | |
| 0EB7 85 17 | STA DEXP | All exponent work finished. | |
| $0EB9 A5 17 | TENPRW | LDA DEXP | Get decimal exponent. |
| 0EBB F0 71 | BEQ FINISH | If it is zero, routine is done | |
| 0EBD 10 61 | BPL MLTPLY | Ir it is plus, go multiply by ten. | |
| 0EBF A2 03 | ONCMOR | LDX $03 | It's minus. Divide by ten. |
| 0EC1 06 04 | BACK | ASL LSB | First shift the accumulator |
| 0EC3 26 03 | ROL NLSB | three bits left. | |
| 0EC5 26 02 | ROL NMSB | ||
| 0EC7 26 01 | ROL MSB | ||
| 0EC9 26 00 | ROL OVFLO | ||
| 0ECB C6 05 | DEC BEXP | Decrease the binary exponent for each left shift. | |
| 0ECD CA | DEX | ||
| 0ECE D0 F1 | BNE BACK | ||
| 0ED0 A0 20 | LDY $20 | Number of trial divisions of $0A into the accumulator giving a $20 = 32 bit quotient. | |
| 0ED2 06 04 | AGAIN | ASL LSB | |
| 0ED4 26 03 | ROL NLSB | ||
| 0ED6 26 02 | ROL NMSB | ||
| 0ED8 26 01 | ROL MSB | ||
| 0EDA 26 00 | ROL OVFLO | ||
| 0EDC 88 | DEY | ||
| 0EDD F0 0E | BEQ OUT | Get out when number of trial divisions reaches $20 = 32. | |
| 0EDF A5 00 | LDA OVFLO | ||
| 0EE1 38 | SEC | Subtract 10 = $0A from partial divident in OVFLO. | |
| 0EE2 E9 0A | SBC $0A | ||
| 0EE4 30 EC | BMI AGAIN | If result is minus, zero into quotient | |
| 0EE6 85 00 | STA OVFLO | Otherwise store result in OVFLO, and set bit to one in quotient. | |
| 0EE8 E6 04 | INC LSB | ||
| 0EEA 18 | CLC | ||
| 0EEB 90 E5 | BCC AGAIN | Try it again. | |
| 0EED A5 00 | OUT | LDA OVFLO | Check once more to see if quotient should be rounded upwards. |
| 0EEF C9 0A | CMP $0A | ||
| 0EF1 90 15 | BCC AHEAD | No. | |
| 0EF3 A2 04 | LDX $04 | Yes. Add one to quotient. | |
| $0EF5 B5 00 | REPET | LDA ACC, X | Get each byte of the accumulator and add the carry from the previous addition. |
| 0EF7 69 00 | ADC $00 | ||
| 0EF9 95 00 | STA ACC, X | ||
| 0EFB CA | DEX | ||
| 0EFC D0 F7 | BNE REPET | ||
| 0EFE 90 08 | BCC AHEAD | What if carry from accumulator occurred? Get mostsignificant byte and put a 1 in bit seven. | |
| 0F00 A5 01 | LDA MSB | ||
| 0F02 09 80 | ORA $80 | ||
| 0F04 85 01 | STA MSB | Result into high byte, and increment the binary exponent. | |
| 0F06 E6 05 | INC BEXP | ||
| 0F08 A5 01 | AHEAD | LDA MSB | Because of three-bit shift at start of division, a one-bit shift (at most) may be required to normalize the mantissa now. |
| 0F0A 30 0A | BMI ARND | ||
| 0F0C 06 04 | ASL LSB | ||
| 0F0E 26 03 | ROL NLSB | ||
| 0F10 26 02 | ROL NMSB | ||
| 0F12 26 01 | ROL MSB | ||
| 0F14 C6 05 | DEC BEXP | If so, also decrement binary exponent. | |
| 0F16 A9 00 | ARND | LDA $00 | Clear overflow byte. |
| 0F18 85 00 | STA OVFLO | ||
| 0F1A E6 17 | INC DEXP | For each divide-by-10, increment the decimal exponent until it is zero. Then its all over. | |
| 0F1C D0 A1 | BNE ONCMOR | ||
| 0F1E F0 0E | BEQ FINISH | ||
| 0F20 A9 00 | MLTPLY | LDA $00 | Clear overflow byte. |
| 0F22 85 00 | STA OVFLO | ||
| 0F24 20 00 0D | STLPLS | JSR TENX | Jump to multiply-by-ten subroutine. |
| 0F27 20 30 0D | JSR NORM | Then normalize the mantissa. | |
| 0F2A C6 17 | DEC DEXP | For each multiply-by-10, decrement the decimal exponent until it's zero. All finished now. | |
| 0F2C D0 F6 | BNE STLPLS | ||
| 0F2E 60 | FINISH | RTS |
| Listing 2. Multiply by Ten Subroutine. | |||
| $0D00 18 | TENX | CLC | Shift accumulator left. |
| 0D01 A2 04 | LDX $04 | Accumulator contains four bytes so X is set to four. | |
| 0D03 B5 00 | BR1 | LDA ACC, X | |
| 0D05 2A | ROL A | Shift a byte left. | |
| 0D06 95 10 | STA ACCB, X | Store it in accumulator B. | |
| 0D08 CA | DEX | ||
| 0D09 10 F8 | BPL BR1 | Back to get another byte. | |
| 0D0B A2 04 | LDX $04 | Now shift accumulator B left once again to get "times four." | |
| 0D0D 18 | CLC | ||
| 0D0E 36 10 | BR2 | ROL ACCB, X | Shift one byte left. |
| 0D10 CA | DEX | ||
| 0D11 10 FB | BPL BR2 | Back to get another byte. | |
| 0D13 A2 04 | LDX $04 | Add accumulator to accumulator B to get A + 4* A = 5* A. | |
| 0D15 18 | CLC | ||
| 0D16 B5 00 | BR3 | LDA ACC, X | |
| 0D18 75 10 | ADC ACCB, X | ||
| 0D1A 95 00 | STA ACC, X | Result into accumulator. | |
| 0D1C CA | DEX | ||
| 0D1D 10 F7 | BPL BR3 | ||
| 0D1F A2 04 | LDX $04 | Finally, shift accumulator left one bit to get 2*5* A = 10* A. | |
| 0D21 18 | CLC | ||
| 0D22 36 00 | BR4 | ROL ACC, X | |
| 0D24 CA | DEX | ||
| 0D25 10 FB | BPL BR4 | Get another byte. | |
| 0D27 60 | RTS |
| Listing 2. Multiply by Ten Subroutine. | |||
| $0D00 18 | TENX | CLC | Shift accumulator left. |
| 0D01 A2 04 | LDX $04 | Accumulator contains four bytes so X is set to four. | |
| 0D03 B5 00 | BR1 | LDA ACC, X | |
| 0D05 2A | ROL A | Shift a byte left. | |
| 0D06 95 10 | STA ACCB, X | Store it in accumulator B. | |
| 0D08 CA | DEX | ||
| 0D09 10 F8 | BPL BR1 | Back to get another byte. | |
| 0D0B A2 04 | LDX $04 | Now shift accumulator B left once again to get "times four." | |
| 0D0D 18 | CLC | ||
| 0D0E 36 10 | BR2 | ROL ACCB, X | Shift one byte left. |
| 0D10 CA | DEX | ||
| 0D11 10 FB | BPL BR2 | Back to get another byte. | |
| 0D13 A2 04 | LDX $04 | Add accumulator to accumulator B to get A + 4*A = 5*A. | |
| 0D15 18 | CLC | ||
| 0D16 B5 00 | BR3 | LDA ACC, X | |
| 0D18 75 10 | ADC ACCB, X | ||
| 0D1A 95 00 | STA ACC, X | Result into accumulator. | |
| 0D1C CA | DEX | ||
| 0D1D 10 F7 | BPL BR3 | ||
| 0D1F A2 04 | LDX $04 | Finally, shift accumulator left one bit to get 2*5*A = 10*A. | |
| 0D21 18 | CLC | ||
| 0D22 36 00 | BR4 | ROL ACC, X | |
| 0D24 CA | DEX | ||
| 0D25 10 FB | BPL BR4 | Get another byte. | |
| 0D27 60 | RTS |
| Listing 3. Normalize the Mantissa Subroutine. | ||||
| $0D 30 18 | NORM | CLC | ||
| 0D 31 A5 00 | BR6 | LDA OVFLO | Any bits set in the overflow byte? Yes, then rotate right. | |
| 0D33 F0 0F | BEQ BR5 | |||
| 0D35 46 00 | LSR OVFLO | No, then rotate left. | ||
| 0D37 66 01 | ROR MSB | |||
| 0D39 66 02 | ROR NMSB | |||
| 0D3B 66 03 | ROR NLSB | |||
| 0D3D 66 04 | ROR LSB | For each shift right, increment binary exponent. | ||
| 0D3F E6 05 | INC BEXP | |||
| 0D41 B8 | CLV | Force a jump back. | ||
| 0D42 50 Ed | BVC BR6 | |||
| 0D44 90 0D | BR5 | BCC BR7 | Did the last rotate cause a carry? Yes, then round the mantissa upward. | |
| 0D46 A2 04 | LDX $04 | |||
| 0D48 B5 00 | BR8 | LDA ACC,X | ||
| 0D4A 69 00 | ADC $00 | Carry is set so one is added | ||
| 0D4C 95 00 | STA ACC,X | |||
| 0D4E CA | DEX | |||
| 0D4F 10 F7 | BPL BR8 | |||
| 0D51 30 DE | BMI BR6 | Check overflow byte once more. | ||
| 0D53 A0 00 | BR7 | LDY $00 | Y will count number of left shifts. | |
| 0D55 A5 01 | BR10 | LDA MSB | Does most-significant byte have a one in bit seven? Yes, get out. | |
| 0D57 30 0D | BMI BR11 | |||
| 0D59 18 | CLC | No. Then shift the accumulator left one bit. | ||
| 0D5A A2 04 | LDX | $04 | ||
| 0D5C 36 00 | BR9 | ROL ACC,X | ||
| 0D5E CA | DEX | |||
| 0D5F D0 FB | BNE BR9 | |||
| 0D61 C8 | INY | Keep track of left shifts. | ||
| 0D62 C0 20 | CPY $20 | Not more than $20 = 32 bits. | ||
| 0D64 90 EF | BCC BR10 | |||
| 0D66 60 | BR11 | RTS | That's it. |
| Listing 4. AIM 65 Input/Output Subroutines. | ||
| $0F30 20 JSR E93C | $0F60 A2 LDX #13 | $0F72 8D STA A44C |
| 0F33 20 JSR F000 | 0F62 8A TXA | 0F75 A2 LDX #01 |
| 0F36 85 STA 06 | 0F63 48 PHA | 0F77 BD LDA A438,X |
| 0F38 20 JSR 0F72 | 0F64 BD LDA A438,X | 0F7A CA DEX |
| 0F3B 20 JSR 0F60 | 0F67 09 0RA #80 | 0F7B 9D STA A438,X |
| 0F3E A5 LDA 06 | 0F69 20 JSR EF78 | 0F7E E8 INX |
| 0F40 60 RTS | 0F6C 68 PLA | 0F7F E8 INX |
| 0F6D AA TAX | 0F80 E0 CPX #15 | |
| $0F85 A2 LDX #12 | 0F6E CA DEX | 0F82 90 BCC 0F77 |
| 0F87 BD LDA A438,X | 0F6F 10 BPL 0F62 | 0F84 60 RTS |
| 0F8A E8 INX | 0F71 60 RTS | |
| 0F8B 9D STA A438,X | ||
| 0F8E CA DEX | $0F9B A2 LDX #13 | |
| 0F8F CA DEX | 0F9D A9 LDA #20 | |
| 0F90 10 BPL 0F87 | 0F9F 9D STA A438, X | |
| 0F92 A9 LDA #20 | 0FA2 CA DEX | |
| 0F94 8D STA A438 | 0FA3 10 BPL 0F9F | |
| 0F97 20 JST 0F60 | 0FA5 60 RTS | |
| 0F9A 60 RTS |